Beaten By Pigeons?

The Monty Hall Problem and why calling someone a bird brain may be a compliment

The game show, Let’s Make a Deal, debuted in 1963 and is still being produced today. On the show, audience members dress up in wacky costumes, hoping to get chosen to be contestants and win prizes. In its heyday with host Monty Hall, it was one of the most popular game shows of all time.

It also spawned a famous illustration of the difficulties we in thinking probabilistically: the Monty Hall Problem. The Monty Hall Problem demonstrates one of the ways pigeons turn out to be smarter than humans. Before we get to that, let’s walk the problem and its solution.

The problem got its name from a common scenario on Let’s Make a Deal.

A contestant gets a choice between three doors (thus, the three doors on my book cover).

Behind one of the doors is a car.

Behind the other two? A goat or similarly ridiculous, worthless prize.

The contestant chooses one of the doors and Monty Hall reveals a goat behind one of the two doors the contestant did not choose. He then offers them a choice: stick with their initial choice or switch to what’s behind the other (unchosen and unopened) door.

Do you switch doors? 

The proper strategy, an accepted part of probability theory, is that you should always switch.

Most people have the initial intuition that it doesn’t matter if you switch doors because with two doors left you must be 50/50 to have the car behind the door you already picked. The car is behind one of the two doors left, after all.

But it actually improves your chances to a 2/3rds chance of getting the car if you switch.

Here’s why: When the contestant initially chooses the doors, there will be a car behind the door they chose one third of the time. That means the door they picked has a 1/3rd chance of having the car behind it and the other two doors combined have a 2/3rds chance of having a door behind one of them. When Monty Hall reveals a goat behind one of the two unchosen doors, the probability of the car being behind the remaining unchosen door remains at 2/3rds since that is the chance the car was behind either of two originally the unchosen doors. (Hint: it really matters that Monty Hall knows where the car is; the reveal isn’t random.)

That’s means that when they are offered to switch, they will improve their odds of getting the car to 2/3rds. If you don’t believe me, try it out a bunch of times and you’ll see that switching wins you the prize twice as often.

Here’s a clear explanation of why it’s correct to switch:

If it seems difficult to understand initially, you’re not alone. Most people stick with their original choice (even after many rounds of the game). According to a review of the literature in a 2018 Psychologica Belgica article, 79-87% won’t switch.

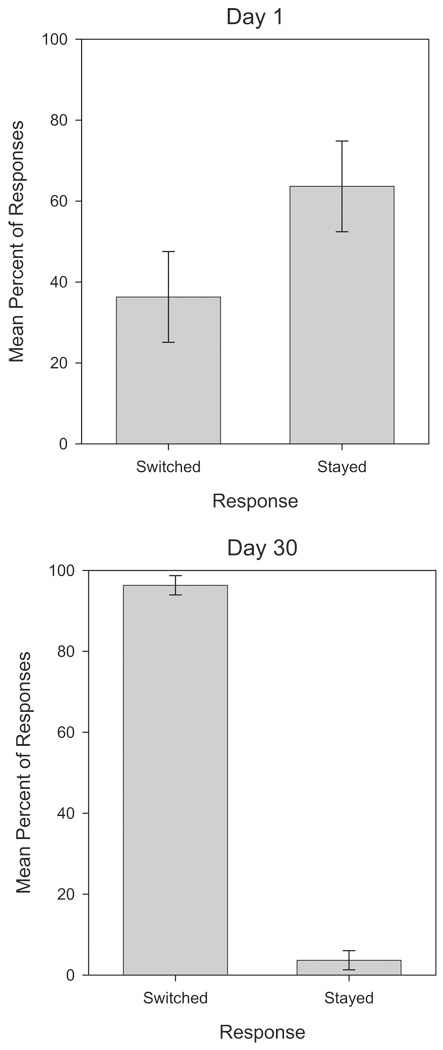
One of the great tidbits in the review: In lab tests of pigeons reported in the Journal of Comparative Psycholog, pigeons pick up on the optimal strategy – switching – more quickly than human subjects. (Pigeons were enticed by “mixed grains,” a reasonable pigeon equivalent of a 1973 Ford Pinto. Humans were competing for high scores.) While human’s are sticky, pigeons learn pretty quickly to switch doors, as shown in the figure below.

The surprising implication is that pigeons seem to solve the puzzle, arriving at the optimal solution while most humans do not.

My guess is that one of the reasons pigeons behave more optimally, separate from the probabilities being hard to calculate, is because they can’t imagine the future in the same way humans can. Last week, I wrote about omission-commission bias and the way we regret bad outcomes much more keenly when they are associated with an action vs. a failure to act.

In the Monty Hall Problem, sticking with the door you already picked is sticking with the status quo, an omission. Switching is an active choice. Like pulling the lever in the Trolley problem. And a bad outcome from switching doors (pulling the lever) is felt much more keenly so humans stick with their door to avoid that regret.

This is where pigeons have it all over humans because pigeons aren’t stuck with the fear of the regret if they switch doors and it turns out the reward was behind their original door.

Take a moment and imagine picking Door #1.

Monty Hall shows you the goat behind Door #2.

He offers you to switch to Door #3. You switch. And it turns out the car was behind Door #1 after all.

You chose the car and then you gave it up. Ugh!

But if you stick with your original door and it turns out the car was behind the new door, it doesn’t feel so bad. That feels more like just dumb luck. Not something you screwed up.

Pigeons can’t think far enough into the future to imagine the car they almost had if they just didn’t switch to the new door. Pigeons are more purely frequentists, not plagued in the same way by these biases or by fear of regret.

So maybe calling a person “bird-brained” is actually insulting to birds rather than the other way around.

(adapted from one of my previous newsletters on annieduke.com)